【Python】MatplotlibとNumPyで数学関数のグラフを描画する

2026年1月11日

概要

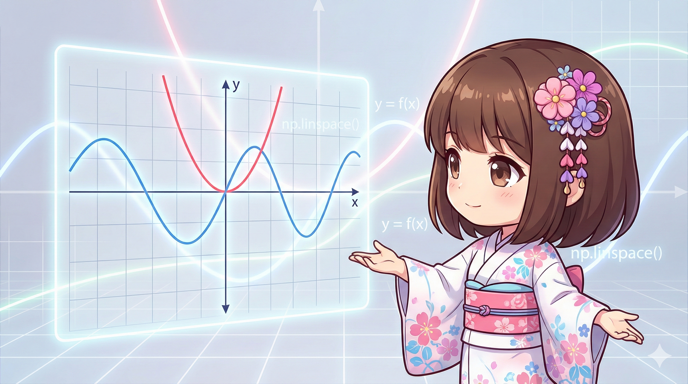
Pythonの数値計算ライブラリNumPyを使用して滑らかな数列データを生成し、Matplotlibで二次関数や三角関数などのグラフを描画するレシピです。手動でリストを作成するのではなく、数式に基づいて大量の座標点を自動生成することで、曲線を綺麗に可視化する方法を解説します。

仕様（入出力）

入力: 定義域（X軸の範囲）、描画したい関数（数式）
出力: 関数の曲線グラフ
要件: matplotlib および numpy ライブラリがインストールされていること

基本の使い方

import matplotlib.pyplot as plt
import numpy as np

# 0から10までを100分割した配列を生成
x = np.linspace(0, 10, 100)
# 配列全体に対して計算（ブロードキャスト機能）
y = np.sin(x)

fig, ax = plt.subplots()
ax.plot(x, y)
plt.show()

コード全文

二次関数と三角関数（コサイン）を同一グラフ上にプロットし、凡例や軸ラベルで整えた完全なコードです。

import matplotlib.pyplot as plt
import numpy as np

def main():
    # 1. データの生成
    # -5 から 5 の範囲を 200分割した等差数列を作成（滑らかな曲線のため）
    x = np.linspace(-5, 5, 200)

    # 2. 関数の定義（NumPyのユニバーサル関数を使用）
    # y1: 二次関数（放物線）
    y1 = 0.5 * x ** 2 - 2
    
    # y2: 三角関数（コサイン波を3倍に振幅）
    y2 = 3 * np.cos(x)

    # 3. グラフの描画設定
    fig, ax = plt.subplots(figsize=(8, 5))

    # 各関数をプロット
    ax.plot(x, y1, label="y = 0.5x^2 - 2", color="blue", linestyle="-")
    ax.plot(x, y2, label="y = 3cos(x)", color="red", linestyle="--")

    # 4. 見た目の調整
    ax.set_title("Function Plot with NumPy")
    ax.set_xlabel("x axis")
    ax.set_ylabel("y axis")
    
    # 原点を通るように軸線を調整（オプション）
    ax.axhline(0, color='black', linewidth=0.5)
    ax.axvline(0, color='black', linewidth=0.5)

    ax.grid(True, linestyle=':', alpha=0.6)
    ax.legend() # 凡例を表示

    # 5. 表示
    plt.show()

if __name__ == "__main__":
    main()

カスタムポイント

np.linspace(start, stop, num): 関数のグラフを描く際、最も重要な関数です。start から stop までを num 個に等分割します。num を大きくするほど曲線が滑らかになります（通常は50〜200程度で十分です）。
NumPyの計算: x がNumPy配列であれば、x ** 2 や np.sin(x) と書くだけで、全要素に対して一括で計算が行われます（ループ処理は不要です）。

注意点

スペルミスに注意 よくある間違いとして linespace（線・スペース）と書いてしまうことがありますが、正しくは linspace（リニア・スペース＝線形空間）です。
arange との使い分け np.arange(start, stop, step) は「刻み幅」を指定しますが、stop を含まないことがあり、分割数を固定しにくいです。グラフ描画には、端点（stop）を確実に含み、分割数を指定できる np.linspace が適しています。
ゼロ除算の考慮 1 / x などの関数を描画する場合、x に 0 が含まれていると実行時警告や無限大（inf）が発生します。範囲をずらすか、特異点を除外する処理が必要です。

バリエーション（任意）

減衰振動グラフ（関数の掛け合わせ）

指数関数と三角関数を掛け合わせた、複雑な波形もNumPyなら1行で計算できます。

import matplotlib.pyplot as plt
import numpy as np

def plot_damped_oscillation():
    # 0 から 20 までの範囲
    t = np.linspace(0, 20, 500)
    
    # 減衰振動の式: e^(-0.1t) * sin(2t)
    y = np.exp(-0.1 * t) * np.sin(2 * t)

    fig, ax = plt.subplots()
    ax.plot(t, y, color='purple')
    
    ax.set_title("Damped Oscillation")
    ax.set_xlabel("Time")
    ax.set_ylabel("Amplitude")
    ax.grid(True)
    
    plt.show()

if __name__ == "__main__":
    plot_damped_oscillation()